「ネズミ算と伝言ゲームで理解する新しい感染症数理モデル
- リンク切れモデル -」
COVID-19の流行(波)は、2020年初旬の第1波に始まり、2022年5月現在までに6つの波がありました。各々の波の開始時には、「感染者数の指数関数的増加」という言葉を良く耳にしませんでしたか?
これは、COVID-19流行を解析するための従来の数理モデル(SIRモデルやその仲間たち)では、感染者数が指数関数的に増加すると想定しているためです。
この記事では、我々のグループで開発した「リンク切れモデル[1], [2]」について、「指数関数的増加」と「リンク切れ」をキーワードとして、具体例を示しながら解説します。そして、COVID-19の拡がりについて考えてみましょう。
「指数関数的増加」=「ネズミ算」
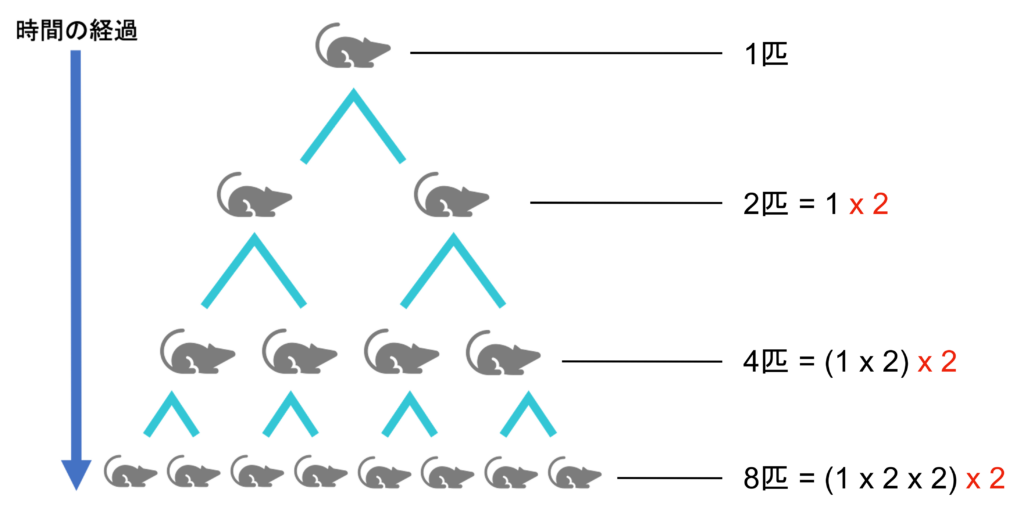
図1:ネズミ算の模式図。1匹の親が平均で2匹の子供を生む場合の様子を表しています。世代が進むにつれて、ネズミの数が倍倍と増えていくことがわかります
図1は、世代が進むにつれてネズミが倍倍で増えていく様子を示しています。1匹から2匹、2匹から4匹と増えますが、このように一定期間で倍倍に増加することを「指数関数的増加」と呼びます。SIRモデルなどの従来の感染症の数理モデルでは、感染者数はネズミ算で増えることを仮定しています。本当にネズミ算的に増えるのであれば、1匹のネズミから10世代後には1024匹、20世代後には100万匹以上に増えるように、1世代の時間が約5日と言われているCOVID-19であれば[3]、100日(20世代)後には、感染者で溢れることになります。これは大変です!そのため、感染者の増加を食い止めるために人流制限などの施策がとられることとなりました。
しかし、感染者は本当にネズミ算で増えるのでしょうか? ネズミ算で増やすには何が必要か?という視点から、一緒に考えてみましょう。
「リンク切れとは? 伝言ゲームを例に」
ここでは、伝言ゲームを例にとって考えます。あるメッセージ(ここでは、「TKG」としましょう)を受け取った人は、未だメッセージを受け取っていない2人に同じメッセージを伝えるというゲームです[4]。先のネズミ算と同様に、10回目の伝言で1024人が新たにTKGというおいしい情報を得ることができます。しかし、図2のように、最初SさんがNさんとIさんにTKGと伝えるはずが、Sさんは怠け者で、Nさんには伝えたが、Iさんには伝え忘れたとしましょう。つまり、Iさんは情報のリンクが切れた状態にあります。このとき、20回目の伝言で何人にメッセージが伝わるか分かりますか? その答えは表1に記載しました。

図2:伝言ゲームでの情報のリンク。SさんからNさんへはTKGというメッセージが伝わるが、Iさんへは伝わらなかった場合。
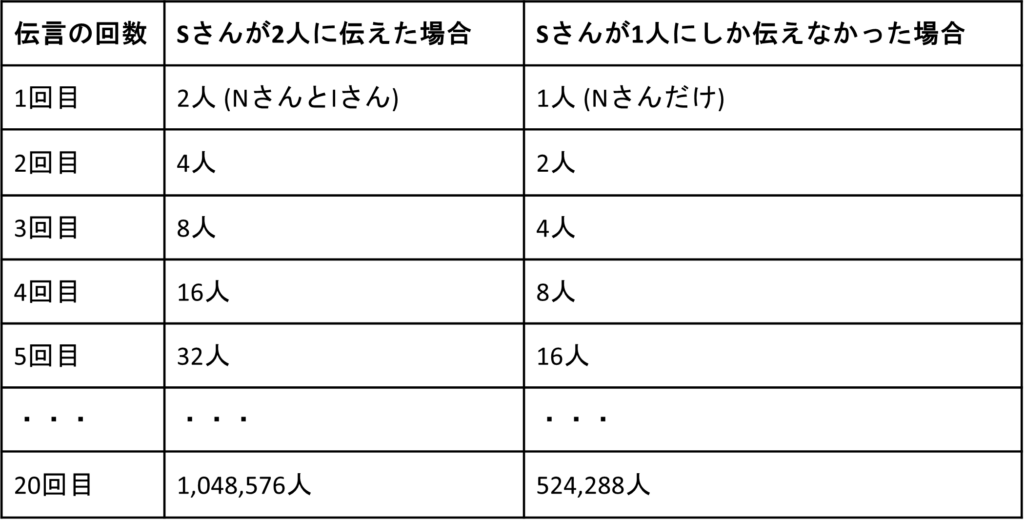
表1:伝言ゲームでの伝言の回数とメッセージを受け取る人の数[5]
表1を見てもらえれば分かるように、20回目にメッセージを受け取る人は、SさんがIさんに伝え忘れたために、約100万人から約50万人に減ってしまっています。たった一人に伝わらなかっただけで、これだけ変化します。重要なことは、リンクが切れたIさんだけがTKGという情報を知らないのではなく、Iさんから繋がる人全体へと影響することです。このアイデアをCOVID-19に適用したのが「リンク切れモデル」です。
「リンク切れモデル」
伝言ゲームの例から得た教訓は、「指数関数的に増加させるためには、全員の努力が必要」ということと「リンクが切れるとその波及効果は極めて大きい」ということです。COVID-19ではどうでしょうか? COVID-19(例えばオミクロン株)では、感染者一人あたり約10人に感染させる可能性があると言われています。指数関数的増加をするのであれば、10倍10倍と増えていくことになりますが、実際の感染者数のデータは感染拡大初期からそのようになっていません。このことは、感染者数の前週比をとっても明らかですし、前回の記事[6]で導入した「K値[7], [8]」を見れば、よりはっきりと分かります[9]。一方で、図3のように「感染のリンクが一定の割合で切れる」と考えると、うまく説明することができます。「一定の割合で」ということは人流抑制の効果ではないということです。

図3:感染症におけるリンク切れの様子。色付きの範囲にいる人たちは感染の脅威から除外されます
感染のリンクが切れる原因として、
●身近に陽性者が出た場合、自身も他者を感染させない行動をとること
●ワクチン接種により免疫を獲得(デルタ株による第5波[10])
などが挙げられます。自身が感染者になった場合に、絶対に10人にうつす義務があると考える人はいないでしょう。このように感染のリンクが切れることは、我々の社会活動において自然なことと考えられます。
さらに、リンク切れモデルに従って計算する(微分方程式を解く)ことで、感染のリンクが切れる確率が[11]、以下の3点を特徴づけることが分かりました:
1.感染者数推移のグラフの形が定まります。
2.基本再生産数(感染者1人から何人に移すかという指標)は、リンクが切れる確率に反比例します。
3.基本再生産数のウイルスがもたらす最終累計感染者数は、に比例します。ここで、はネイピア数と呼ばれ、自然対数の底を表します。
新しい感染症数理モデルであるリンク切れモデルについて、モデル構築のアイデアを中心に紹介してきました。従来の感染症数理モデルでは、感染者数の指数関数的増加を仮定しているため、人流抑制などの対策が必要と考えられてきました。一方で、リンク切れモデルでは一様な人流抑制ではなく、行動の質が重要であることを示しています。とりわけ、自身が感染者である可能性がある場合に、家族や身近な人以外との濃厚接触機会を無くせば、感染させなかった人だけでなく、その人からつながる可能性のあった全ての人を救う行為となります。このことを頭の片隅に置いて、これまでの日常を取り戻していただければと願います。
参考文献・補足
[1]Y. Ikeda, K. Sasaki, T. Nakano, “A New Compartment Model of COVID-19 Transmission: The Broken-Link Model”, International Journal of Environmental Research and Public Health:https://www.mdpi.com/1660-4601/19/11/6864
[2]SpringX 超学校 CiDER(大阪大学感染症総合教育研究拠点) × ナレッジキャピタル, 正しく学ぶ! 感染症から「いのち」と「くらし」を守る講座, “第8回 感染者数推移から解き明かす新型コロナの流行メカニズム”
[3]COVID-19感染報告者数に基づく簡易実効再生産数推定方法 (IASR Vol. 42 p128-129: 2021年6月号), https://www.niid.go.jp/niid/ja/diseases/ka/corona-virus/2019-ncov/2502-idsc/iasr-in/10465-496d04.html
[4]伝言ゲームで面白いのは、正確にメッセージが伝わらず、最終的にはめちゃくちゃなメッセージになっているところですが、ここでは正確にメッセージが伝わっていることにしましょう
[5]2を底とする対数でメッセージを受け取る人数を書き直すと、ある法則が現れます。2を底とする対数は、で表し、その意味は(2を回かけるとになる)です。にメッセージを受け取る人数を代入してみましょう
[6]「K値とは何か?」
[8]佐々木健志, 池田陽一, 中野貴志 著, 「K値とは何か–新型コロナウイルスの拡散と収束–」, 物理科学,この1年 2022, 丸善出版, pp. 172-177.
[9]指数関数的に増加する場合、K値は一定になりますが、実際のデータでは単調に減少することが分かります。興味のある方は是非、K値のグラフを作ってみて下さい。百聞は一見に如かず
[10]アルファ株やデルタ株に対するmRNAワクチンの有効性については、国立感染症研究所の報告 https://www.niid.go.jp/niid/ja/2019-ncov/2484-idsc/10966-covid19-71.html が参考になります。また、ワクチン摂取がリンクの切れる確率へどのように影響したかは[2]で報告しています
[11]正確には期待値・平均値です


