「K値とは何か?」
COVID-19の感染拡大の状況をリアルタイムで把握し、その変化の兆候をいち早く検知するための新しい指標がK値です1,2)。その詳細を説明する前に一般的に「運動」の「変化」を捉えるためには、どのような方法があるかおさらいしてみましょう。
まず日常生活で一番馴染みが深い指標として「速度」があります。自動車には最初から速度メーターがついていますが、原理的には位置と時間の詳細な測定データがあれば、そのグラフの接線の傾きから求まります(図1)。つぎに、接線の傾きから求めた速度を縦軸にして、もう一度接線の傾きを求めると加速度となります(図2)。空気抵抗のような外力が無視できるような理想的な状況では、万有引力の法則により、地表面付近の鉛直方向の運動は一定の加速度を示します。
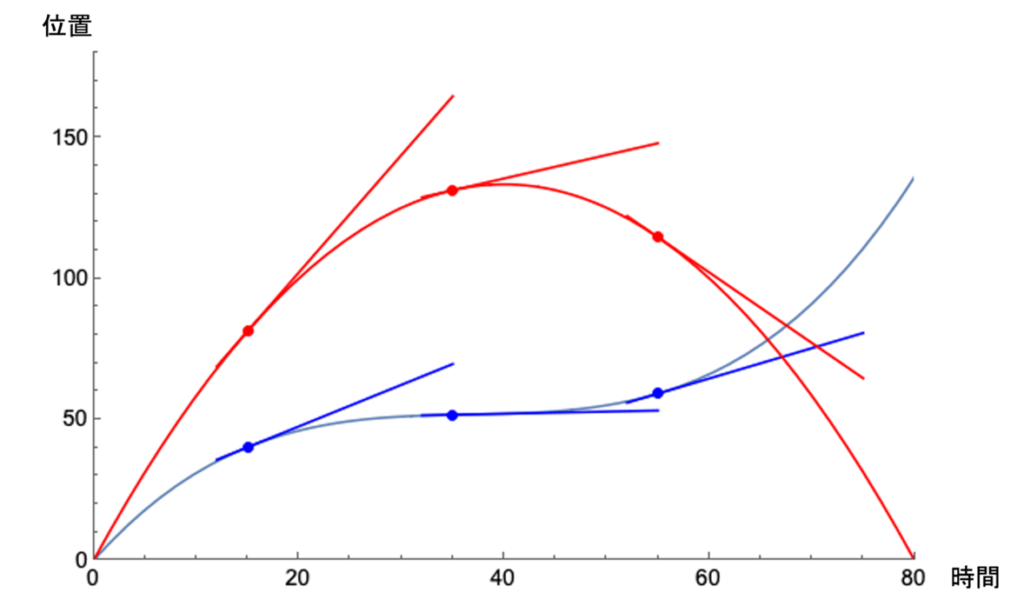
図1:位置と時間のグラフ。時間0での初期位置を0としています。曲線の各時点で接線を引いた際に、その接線の傾きが速度となります。
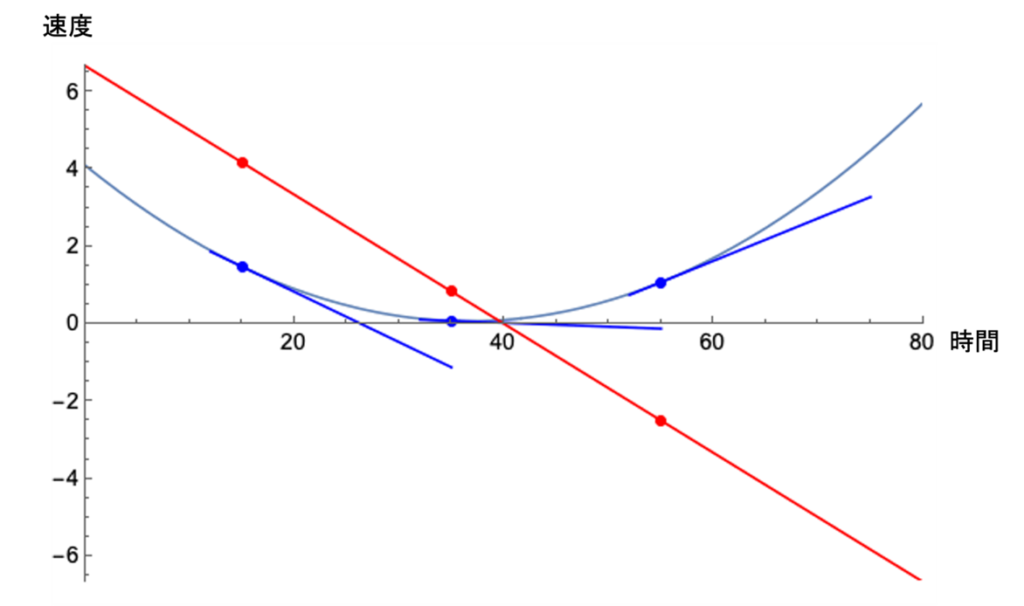
図2:速度と時間のグラフ。各時点での接線の傾きが加速度を表します。赤と青の曲線はそれぞれ図1の同じ色の曲線に対応した量となります。
次に何も「外力」が働かない場合に指数関数的な変化をする現象に対して、どのような「速度計」が便利かを考えてみましょう。指数関数的な変化をするものには細菌の増殖から宇宙の膨張、さらには利率が一定の複利預金まで色々な例がありますが、その特徴は、縦軸が1メモリ毎に10倍に増えていく対数グラフで、注目している量(細菌数、宇宙の大きさ、預金残高)の時間変化をプロットすると直線になるということです。
COVID-19の感染者数も感染拡大初期の一定期間は指数関数的に増えていくと仮定されていたため3)、図3のように横軸を時間、縦軸を累計感染者数とした対数グラフでの接線の傾きを近似的に求める方法としてK値を提案しました。実効再生産数が一定で、累計感染者数が指数関数的に増加すると、K値は一定値を取ります。例えば,累計感染者数が1週間に2倍のペースで増加を続けるとK値は0.5を取り続けます。一方で,世界の各国のK値推移を観察すると、社会的活動が制限される前の感染拡大初期から一定値とならずに、単調に減少していることがわかりました。これは感染拡大率が時間と共に減少していることを示します。
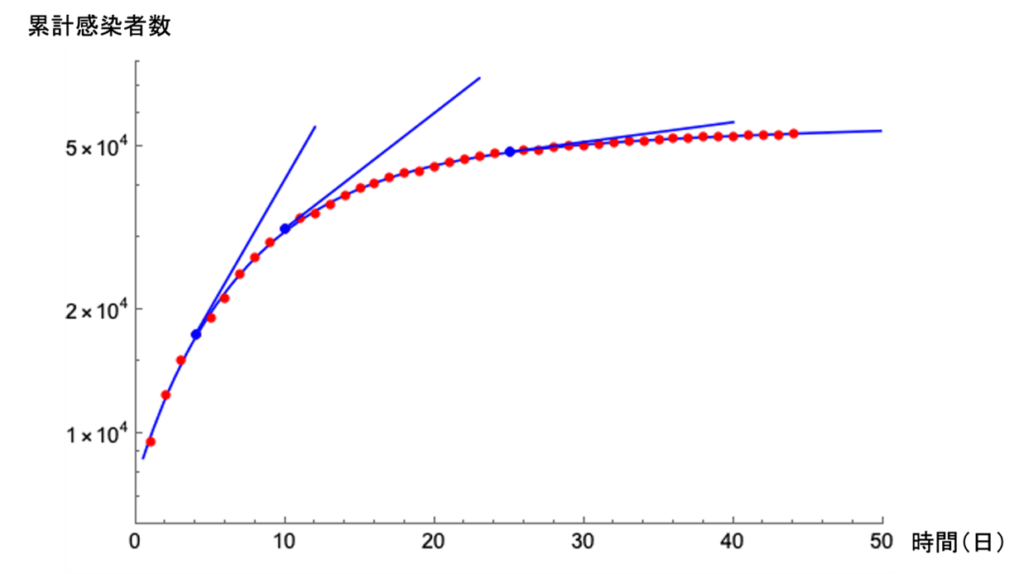
図3:ある地域におけるCOVID-19の累計感染者数と時間に関する対数グラフ。各時点での接線の傾きがK値に対応する量となります。測定基準日を0日としています。
感染拡大率の単調な減少を生み出すメカニズムは、長らくわからなかったのですが、ヒトからヒトへ伝播する感染症の「リンク切れ」という効果を、代表的な感染症数理モデルであるSIRモデルに導入することで、K値の単調減少が説明可能であることが。さらに、各種の感染防止対策によってリンク切れ確率が変化した場合に、感染の規模や収束の速さがどのように変化するかを定量的に求めることが可能となりました4)。詳しくはハイブリッドセミナーをご覧ください。
参考文献
2)佐々木健志, 池田陽一, 中野貴志 著, 「K値とは何か–新型コロナウイルスの拡散と収束–」,物理科学, この1年 2022, 丸善出版, 2022, pp172-177.
3)小林鉄郎, 西浦博 著, 「感染症数理モデル入門/SIRコンパートメントモデルと基本再生産数」, 数学セミナー 2020年9月号, 日本評論社, 2020, pp14-18.
■詳しくはこちら


